Illustrations of non-Euclidean geometry in virtual reality

PubDate: Aug 2020

Teams: msmathcomputer

Writers: Martin Skrodzki

PDF: Illustrations of non-Euclidean geometry in virtual reality

Abstract

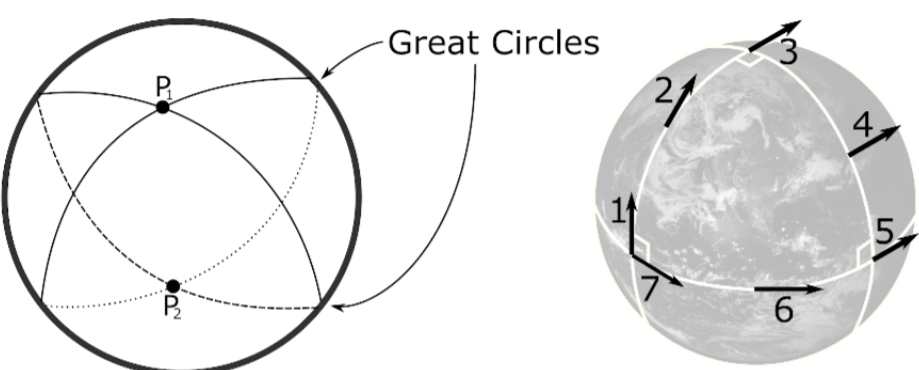
Mathematical objects are generally abstract and not very approachable. Illustrations and interactive visualizations help both students and professionals to comprehend mathematical material and to work with it. This approach lends itself particularly well to geometrical objects. An example for this category of mathematical objects are hyperbolic geometric spaces. When Euclid lay down the foundations of mathematics, his formulation of geometry reflected the surrounding space, as humans perceive it. For about two millennia, it remained unclear whether there are alternative geometric spaces that carry their own, unique mathematical properties and that do not reflect human every-day perceptions. Finally, in the early 19th century, several mathematicians described such geometries, which do not follow Euclid’s rules and which were at first interesting solely from a pure mathematical point of view. These descriptions were not very accessible as mathematicians approached the geometries via complicated collections of formulae. Within the following decades, visualization aided the new concepts and two-dimensional versions of these illustrations even appeared in artistic works. Furthermore, certain aspects of Einstein’s theory of relativity provided applications for non-Euclidean geometric spaces. With the rise of computer graphics towards the end of the twentieth century, three-dimensional illustrations became available to explore these geometries and their non-intuitive properties. However, just as the canvas confines the two-dimensional depictions, the computer monitor confines these three-dimensional visualizations. Only virtual reality recently made it possible to present immersive experiences of non-Euclidean geometries. In virtual reality, users have completely new opportunities to encounter geometric properties and effects that are not present in their surrounding Euclidean world.