Sparse-to-Dense Multi-Encoder Shape Completion of Unstructured Point Cloud

PubDate: February 2020

Teams: Shandong University of Science and Technology;Shenzhen Institutes of Advanced Technology

Writers: Yanjun Peng; Ming Chang; Qiong Wang; Yinling Qian; Yingkui Zhang; Mingqiang Wei; Xiangyun Liao;

PDF: Sparse-to-Dense Multi-Encoder Shape Completion of Unstructured Point Cloud

Abstract

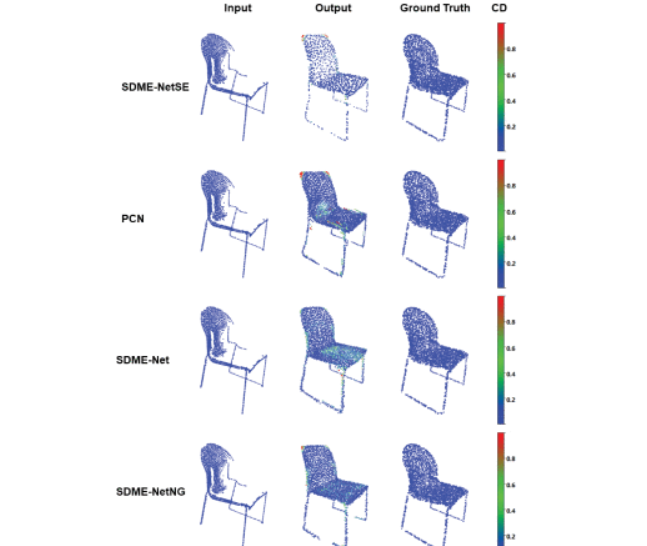
Unstructured point clouds are a representative shape representation of real-world scenes in 3D vision and graphics. Incompletion inevitably arises, due to the way the set of unorganized points is captured, e.g., as fusion of depth images, merged laser scans, or structure-from-x. In this paper, an end-to-end sparse-to-dense multi-encoder neural network (termed an SDME-Net) is proposed for uniformly completing an unstructured point cloud with its shape details preserved. Unlike most existing learning-based shape completion methods that are enforced on the representations of 2D images and 3D voxelization of point clouds, and require priors of the underlying shape’s structures, topologies and annotations, the SDME-Net is implemented on the incomplete and even noisy point cloud without any transformation, and makes no specific assumptions about the incompletion distribution and geometry features in the input. Specifically, the defective point cloud is completed and optimized in a sparse-to-dense manner of two-stages. In the first stage, we generate a sparse but complete point cloud based on a bistratal PointNet, and in the second stage, we yield a dense and high-fidelity point cloud by encoding and decoding the sparse result in the first stage using PointNet++. Meanwhile, we combine the distance loss and repulsion loss to generate more uniformly distributed output point clouds closer to the ground-truth counterparts. Qualitative and quantitative experiments on the public ShapeNet dataset illustrate that our approach outperforms the state-of-art learning-based point cloud shape completion methods in terms of real structure recovery, uniformity, and noise/partiality robustness.