AutoInt: Automatic Integration for Fast Neural Volume Rendering

PubDate: May 2021

Teams: Stanford University

Writers: David B. Lindell, Julien N. P. Martel, Gordon Wetzstein

PDF: AutoInt: Automatic Integration for Fast Neural Volume Rendering

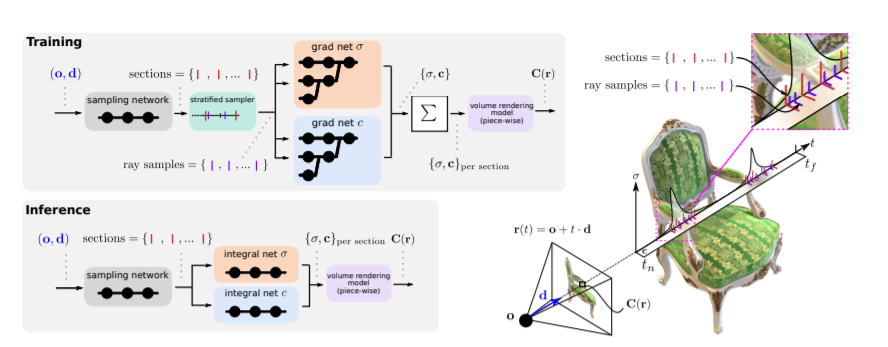
Abstract

Numerical integration is a foundational technique in scientific computing and is at the core of many computer vision applications. Among these applications, neural volume rendering has recently been proposed as a new paradigm for view synthesis, achieving photorealistic image quality. However, a fundamental obstacle to making these methods practical is the extreme computational and memory requirements caused by the required volume integrations along the rendered rays during training and inference. Millions of rays, each requiring hundreds of forward passes through a neural network are needed to approximate those integrations with Monte Carlo sampling. Here, we propose automatic integration, a new framework for learning efficient, closed-form solutions to integrals using coordinate-based neural networks. For training, we instantiate the computational graph corresponding to the derivative of the network. The graph is fitted to the signal to integrate. After optimization, we reassemble the graph to obtain a network that represents the antiderivative. By the fundamental theorem of calculus, this enables the calculation of any definite integral in two evaluations of the network. Applying this approach to neural rendering, we improve a tradeoff between rendering speed and image quality: improving render times by greater than 10 times with a tradeoff of slightly reduced image quality.